Mechanizm zapadkowy - rozkład sił

[stanfor27]

Witam, mam pewien problem, potrzebuję zrobić rozkład sił w mechanizmie zapadkowym (konkretnie w tym czerwonym kółku) i nie do końca wiem jak się za to zabrać. Jedyna przyłożona siła to siła pracownika - 300 N. Na pierwszym zdjęciu widać mechanizm w przekroju, nie wiem czy dokładnie widać - jest tam sprężyna dociskowa, popychacz (zakończenie stożkowe na końcu) i widełki na które naciska. Na drugim zdjęciu pokazałem inny przekrój tego mechanizmu. Proszę o pomoc

[gulonsza]

Wydaje mi się, że rozkład sił w tym obszarze będzie zależał tylko od wstępnego napięcia sprężyny. Siła z jaką działa pracownik na ramię mechanizmu zapadkowego nie ma znaczenia.

Oto cały skomplikowany wzór na siłę

F=k Δx

gdzie:
F – siła rozciągająca [N],
Δx – wydłużenie [m],
k – współczynnik sprężystości sprężyny w N/m.
Możesz się spotkać ze znakiem minus "-" przed współczynnikiem k. Minus ten oznacza że siła ma zwrot przeciwny do wychylenia.

[BYDGOST]

Skoro elementy oporowe, w miejscach zaznaczonych na czerwono zamocowane są obrotowo, to ten podnośnik nie będzie działał.

[stanfor27]

potrzebuję wyliczyć siłę Fy - uginającą sprężynę, podczas przyłożenia siły Fr', która powoduje powstanie sił pokazanych na rysunku (przy zębie) na skutek czego widełki będą odpychać się od kolejnych zębów, muszę powiązać te siły z siłą Fy, brakuje mi już na to pomysłów, jeśli ktoś ma jakąś koncepcję będę wdzięczny

[BYDGOST]

Tu trzeba skorzystać z zasady prac przygotowanych i pójść w kierunku projektowania krzywek.

[upadły_mnich]

nie wiem czy chcesz liczyc wartość chwilową tej siły czy analizować jak ona sie zmienia wraz z położeniem dźwigni, zapadki itp.
Przypuszczam, że to pierwsze.
W tym wypadku pomoże Ci zasada, że siła na styku 2 przedmiotów działa prostopadle do powierzchni (sorry za nietechniczny język)
U Ciebie:
Siła wypadkowa=suma wektorowa Fo` i Fz działająca na styku zęba i zapadki jest prostopadła do powierzchni zapadki. Tak czy inaczej musisz mieć więcej wymiarów aby to pchnąć.
A dalej po kolei:
Moment na osi zapadki, siła na styku tłoczek-zapadka (z podobnej co wyżej zasady) i siła na sprężynie.

Nie mogę załączyć pliku - wyszedłem z wprawy.

[gulonsza]

Ja bym się do tego zabrał tak.
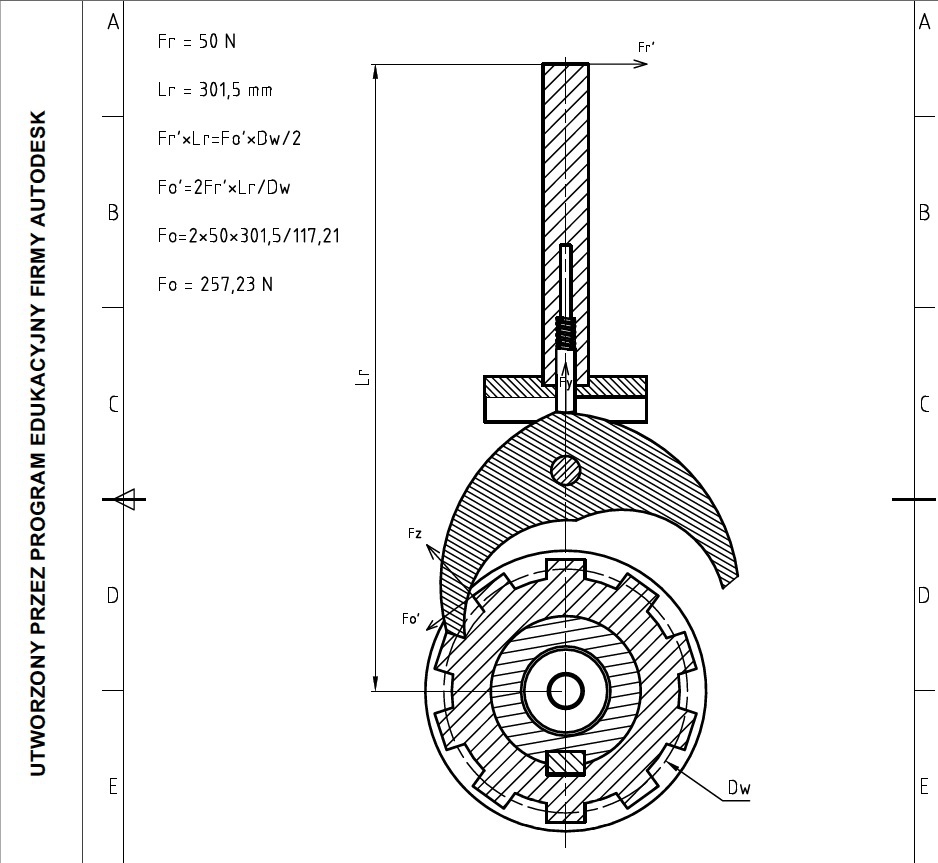
1. Rozkładasz siły Fz i Fo na składowe tak aby działały one w kierunkach działania sił Fr i Fy. W kierunku Fr będziesz miał -Fz sin(alfa)+Fo cos(alfa), w kierunku działania sił Fy masz Fz cos(alfa)-Fo sin(alfa).
2. Określasz kąt alfa żebyś mógł obliczyć wartość funkcji trygonometrycznej. Albo dzielisz okrąg na ilość części albo w tym przypadku określasz ją z Autocada.
3. Następnie piszesz równania równowagi. Ja rozwiązałbym to zagadnienie jako statyczne, czyli suma wszystkich sił działających w danej osi musi równać się 0.
Równanie równowagi były by następujące.
Dla osi poziomej (nazwijmy ją x): Fr-Fzsin(alfa)-Focos(alfa)=0
Dla osi pionowej (nazwijmy ją y): Fzcos(alfa)-Fosin(alfa)+Fy=0
Jeszce równanie momentów musi się równać 0: Fz*Lr+Fzsin(alfa)*ramię+Focos(alfa)*ramię+Fosin(alfa)*ramię-Fzcos(alfa)*ramię=0

Z pierwszego równania wyliczasz Fz sin(alfa), bo kąt znajdziesz Fr i Fo masz obliczoną.
Potem układ równań i obliczasz siły Fz cos (alfa) i siłę Fy.

Otrzymujesz wypadkową wartość siły Fy. Ona również będzie się rozkładała na składowe działające wzdłuż osi x i y w zależności od punktu styku z krzywką. Wektor zawsze będzie prostopadły do płaszczyzny więc z tym nie powinno być problemów w znalezieniu wartości chwilowej.
Jedynie co musisz to sprawdzić, czy się nie pomyliłem przy funkcjach trygonometrycznych, zweryfikować kierunki działania sił, znaleźć kąt alfa i ramie na jakim działają siły w równaniu momentów. Mam nadzieję, że obliczenia ujrzymy wkrótce
Mam nadzieję, że