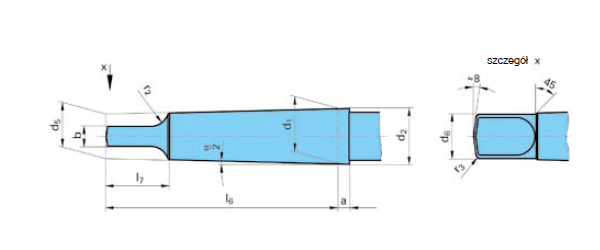
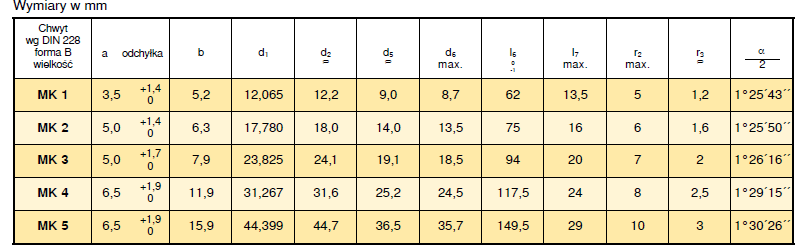
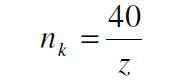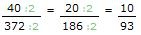krzysiek gil pisze:zostalo mi jeszcze wytoczyć te dwa pierścienie na te dwa noniusze z podziałką w minutach i w sekundach, problem w tym ze nie wiem jak to przerzucić na podzielnice żeby dobrać odpowiednia tarczkę do nacinania kresek
Na podzielnicy(fabrycznej) robi się to dokładnie tak jak byś kolego dzielił okrąg na zadaną ilość działek. co sobie obliczymy.
Najpierw jednak musimy wiedzieć ile stopni ma zawierać skala główna, czyli o ile stopni obróci się stolik robiąc jeden pełny obrót pokrętłem, a to zależy od przełożenia ślimak/ślimacznica naszego stołu, jak pisałem wyżej, Na przykład,
- jeśli jest to
40:1, to pełny obrót pokrętła przesunie stół o : 360°:40 =
9°,
- jeśli przełożenie
72:1 to pełny obrót pokrętła wyniesie : 360°:75 =
5°,
- a jak przełożenie
90:1, to obrót pokrętła wyniesie : 360°:90 =
4°
(nawiasem jak widać, im większe przełożenie tej podzielnicy, tym dokładniejszą skalę można zrobić - większe działki lub więcej ich się zmieści w 1° skali),
i dopiero wtedy możemy każdy stopień skali głównej podzielić sobie na minuty, czyli obliczyć ilość działek na głównej skali. Co będzie bazą do obliczenia ilości otworków w tarczy podzielnicy wykonawczej nasze skale
Jakie przełożenie ślimak/ślimacznica ma stół kolegi do którego mamy wykonać te skale ?, bo bez tego to tylko można rozważania teoretyczne uprawiać przyjmując jakieś założenia.
Np dla 72:1
Jeżeli skala główna (360°) ma mieć X działek, np
ma skalę główną 5°/1obr., 120 działek, jedna działka to 2'(minuty)

To podzielnicę do wykonania bębenka ustawiamy na podział okręgu na 120 części, wg wzorów na obliczanie ilości otworków w tarczy. jest to:

masz, o ile pamiętam, podzielnicę z przełożeniem 40:1 więc

Tu akurat sprawa jest prosta bo dzieli się ładnie na 3, alę że nie ma tarczy z 3 otworami, to trzeba zastosować taką z ilością otworków będącą wielokrotnością liczby 3 np
(typowe tarcze mają:
I – 15, 16, 17, 18, 19, 20,
II – 21, 23, 27, 29, 31 i 33,
III – 37, 39, 41, 43, 47 i 49. ) jak widać tarcza z 33 jest tu adekwatna (przestawianie co 11 otw.), poza tym 27(co 9), 15(co 5), 39(co 13), itd..
Natomiast noniusz posiadający x działek zajmujący rzeczywisty kąt okręgu 360° (a nie w/g wskazań podziałki skali głównej),

to najpierw musimy obliczyć ile takich x-działkowych noniuszy ma się zmieścić na okręgu 360°, czyli jak widać na zdjęciu
pokrywają się działki "0" noniusza i skali głównej, oraz 13 działka noniusza(130") i działka 30"(0,5°) skali głównej
(powinno być 30' - powyżej, wkradł się błąd, zapisałem - 30
" zamiast 30
', przepraszam kolegów)
a 0,5°(30') naszej skali zajmuje na okręgu rzeczywisty kąt 360°:10 = 36°
czyli zmieścimy takich 13-działkowych noniuszy 10, co daje działek na 360° okręgu :
10 x 13(dz) = 130dz/360° czyli musimy poszukać tarczy z ilością otworów :


a jako że nie mamy tarczy z 13-toma otworami, to musimy poszukać krotności, czyli przykładowo 3x(mianownik)13=
39, a taka jest
III – 37,
39, 41, 43, 47 i 49, i na niej musimy przestawiać wskazówki o otworków: 3x4(licznik)=
12
Oczywiście nacinamy nie na całym okręgu wszystkie 130 działek, tylko te nas interesujące 13(+3 dodatkowe jak na zdjęciu bębenka noniusza)
dla innych ratio postępujemy analogicznie.
W razie pytań proszę pisać... (i poprawiać jeśli gdzieś dałem ciała..

)









 a jako że nie mamy tarczy z 13-toma otworami, to musimy poszukać krotności, czyli przykładowo 3x(mianownik)13=39, a taka jest
a jako że nie mamy tarczy z 13-toma otworami, to musimy poszukać krotności, czyli przykładowo 3x(mianownik)13=39, a taka jest


 (nie wgrywa się zdj.)
(nie wgrywa się zdj.)