toczenie promienia na tokarce CNC sinumeryk840
-
kolorówka
Autor tematu - Nowy użytkownik, używaj wyszukiwarki

- Posty w temacie: 5
- Posty: 5
- Rejestracja: 20 lis 2017, 16:33
Re: toczenie promienia na tokarce CNC sinumeryk840
dzięki za pomoc a efekty zobaczę jutro bo z tym zawieszeniem R224 będzie problem a o pomyłce nie może być mowy mam tylko jedno podejście inaczej mam przegrane
-
Steryd
- Lider FORUM (min. 2000)

- Posty w temacie: 1
- Posty: 4396
- Rejestracja: 13 lut 2017, 19:34
- Lokalizacja: Szczecin
Re: toczenie promienia na tokarce CNC sinumeryk840
dużo więcej jest na stronie 209.
Czy ktoś jeszcze pamięta cykle konturowe? Szczerze mówiąc jak dla mnie nie do zaprogramowania offline, za to na tokarce pewnie byś znalazł odpowiedni wzorzec i go wykonał w 30 sekund.
Czy ktoś jeszcze pamięta cykle konturowe? Szczerze mówiąc jak dla mnie nie do zaprogramowania offline, za to na tokarce pewnie byś znalazł odpowiedni wzorzec i go wykonał w 30 sekund.
Można?
Morzna!!!
Morzna!!!
-
jasiu...
- Lider FORUM (min. 2000)

- Posty w temacie: 4
- Posty: 5776
- Rejestracja: 14 lip 2007, 19:02
- Lokalizacja: Westfalia
Re: toczenie promienia na tokarce CNC sinumeryk840
No dobra, trochę zabawy w liczenie. Pozwól, że odwrócę twój rysunek o 90 stopni w prawo, bo dla mnie do toczenia tak wygodniej. Przyjmuję zero na powierzchni czołowej (w Z), Wtedy wszystkie wymiary w Z będą ujemne (w lewo od tej płaszczyzny jest przygotówka). Oczywiście zero X jest w osi.
Na początek punkty, przez które przechodzi R2.5, czyli początek X44.65 Z-6.07 i koniec X45.9 i Z6.75
Przez ten ostatni punkt przechodzi też R224. W tym punkcie z zawieszenia R2.5 do zawieszenia R224 można przeprowadzić linię prostą, skoro jeden przechodzi w drugi i są styczne.
Poprowadźmy sobie pomiędzy tymi punktami linię. Możemy znaleźć jej długość (odległość dwóch punktów) skoro linia ma przyrost w X 45.9-44.65=1.25 i w Z 6.75-6.07=0.68, to z twierdzenia pitagorasa mamy długość linii √ (Δ x ² + Λ y ² ), a więc √ (1.25 ² +0.68 ² ) = √ (1.5625+0.4624)= √ 2.0249=1.42298981
Możemy też z tangensa obliczyć sobie nachylenie tej linii. atan(0.68/1.25)=atan(0.544)=28.546190731043 stopnia. Oczywiście plus 90 stopni, bo mamy odwrócony rysunek.
Narysujmy sobie to:
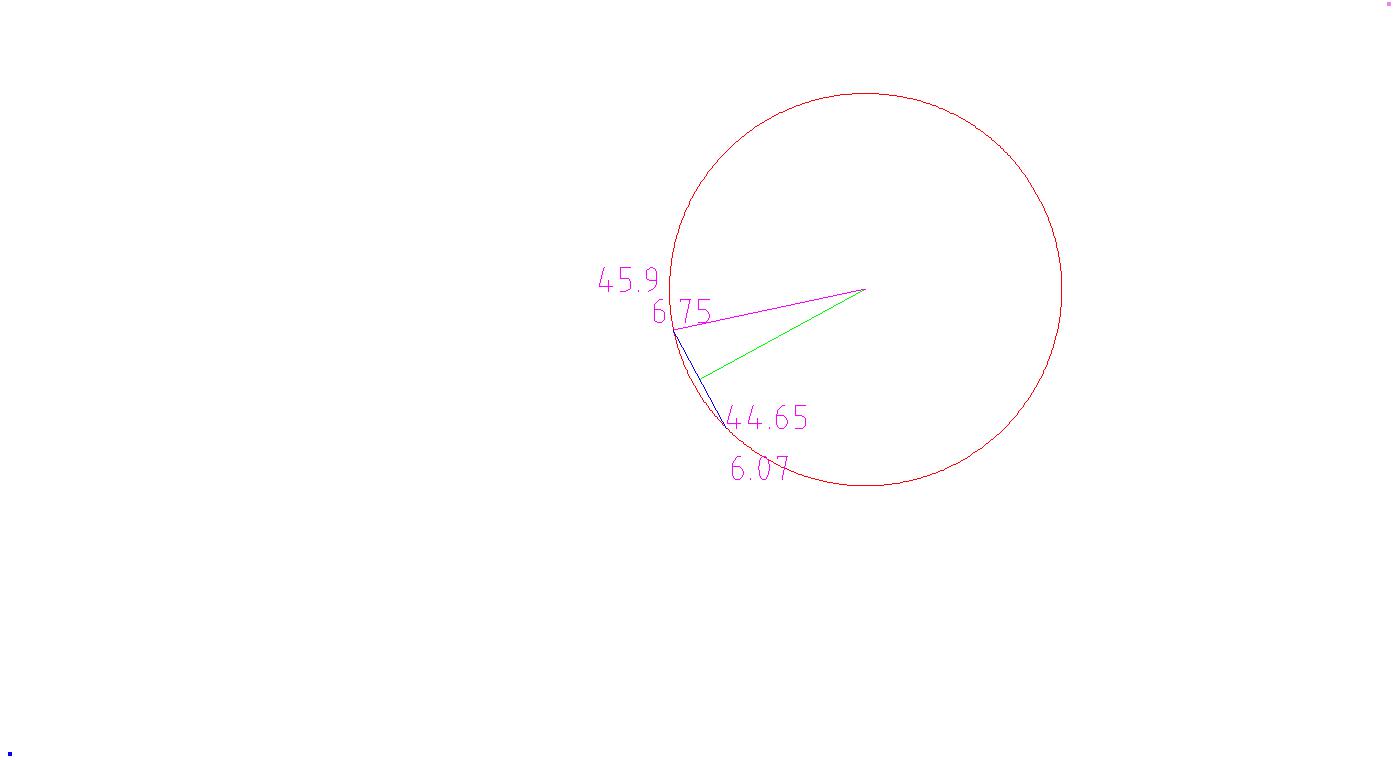
Przeanalizujmy.
Granatowa linia pomiędzy punktami, to linia, której kąt nachylenia do układu i długość właśnie wyliczyliśmy. Różowa, to promień wynoszący 2.5. Zielona, to dwusieczna łuku. Zrobił się trójkąt prostokątny, z różowej (R2.5), połowy wyliczonej powyżej 1.42298... (czyli ok. 0.7115) i zielonej (nie znamy długości, ale wiemy, że jest prostopadła do granatowej, bo to trójkąt prostokątny).
No właśnie, to pod jakim kątem jest ta fioletowa? Kąt pomiędzy granatową i fioletową znajdziemy z cosinusa. Przyprostokątna przy kącie, czyli 0.7115 dzielona przez 2.5 to daje 0.2846 a arcus cosinus z tego, to 73.46505984641 stopnia.
Mamy nachylenie granatowej do układu, mamy różnicę w kącie pomiędzy granatową i fioletową, czyli znajdziemy nachylenie fioletowej. Moim zdaniem (90+28.5462)=118.5462 (ciut zaokrągliłem). Plus 73.4651 = 192.0113 (i widać, że około 12 stopni ten kąt ma)
No tak, ale na przedłużeniu fioletowej leży punkt zawieszenia promienia R224. Trudno go obliczyć? Moim zdaniem nie. Mamy początek w punkcie 6.75;49.5, mamy długość prostej - 224. Czyli jedna współrzędna to sinus wyliczonego kąta razy długość promienia, a druga razy cosinus.
Moim zdaniem dalej tłumaczyć sensu nie ma, co do czego (znaczy do współrzędnych powyższego punktu końca promienia R2.5) trzeba dodać.
Pobawiłem się, bo uważam, że trzeba co niektórym uświadomić, że bez dobrej znajomości geometrii w naszym fachu, gdzie sporo czasem trzeba przeliczać, ciężko.
Na początek punkty, przez które przechodzi R2.5, czyli początek X44.65 Z-6.07 i koniec X45.9 i Z6.75
Przez ten ostatni punkt przechodzi też R224. W tym punkcie z zawieszenia R2.5 do zawieszenia R224 można przeprowadzić linię prostą, skoro jeden przechodzi w drugi i są styczne.
Poprowadźmy sobie pomiędzy tymi punktami linię. Możemy znaleźć jej długość (odległość dwóch punktów) skoro linia ma przyrost w X 45.9-44.65=1.25 i w Z 6.75-6.07=0.68, to z twierdzenia pitagorasa mamy długość linii √ (Δ x ² + Λ y ² ), a więc √ (1.25 ² +0.68 ² ) = √ (1.5625+0.4624)= √ 2.0249=1.42298981
Możemy też z tangensa obliczyć sobie nachylenie tej linii. atan(0.68/1.25)=atan(0.544)=28.546190731043 stopnia. Oczywiście plus 90 stopni, bo mamy odwrócony rysunek.
Narysujmy sobie to:

Przeanalizujmy.
Granatowa linia pomiędzy punktami, to linia, której kąt nachylenia do układu i długość właśnie wyliczyliśmy. Różowa, to promień wynoszący 2.5. Zielona, to dwusieczna łuku. Zrobił się trójkąt prostokątny, z różowej (R2.5), połowy wyliczonej powyżej 1.42298... (czyli ok. 0.7115) i zielonej (nie znamy długości, ale wiemy, że jest prostopadła do granatowej, bo to trójkąt prostokątny).
No właśnie, to pod jakim kątem jest ta fioletowa? Kąt pomiędzy granatową i fioletową znajdziemy z cosinusa. Przyprostokątna przy kącie, czyli 0.7115 dzielona przez 2.5 to daje 0.2846 a arcus cosinus z tego, to 73.46505984641 stopnia.
Mamy nachylenie granatowej do układu, mamy różnicę w kącie pomiędzy granatową i fioletową, czyli znajdziemy nachylenie fioletowej. Moim zdaniem (90+28.5462)=118.5462 (ciut zaokrągliłem). Plus 73.4651 = 192.0113 (i widać, że około 12 stopni ten kąt ma)
No tak, ale na przedłużeniu fioletowej leży punkt zawieszenia promienia R224. Trudno go obliczyć? Moim zdaniem nie. Mamy początek w punkcie 6.75;49.5, mamy długość prostej - 224. Czyli jedna współrzędna to sinus wyliczonego kąta razy długość promienia, a druga razy cosinus.
Moim zdaniem dalej tłumaczyć sensu nie ma, co do czego (znaczy do współrzędnych powyższego punktu końca promienia R2.5) trzeba dodać.
Pobawiłem się, bo uważam, że trzeba co niektórym uświadomić, że bez dobrej znajomości geometrii w naszym fachu, gdzie sporo czasem trzeba przeliczać, ciężko.













