cnc.info.pl - FORUM CNC

Witam
Jak można obliczyć moduł koła stożkowego o zębach prostych?
Przeszukałem już wiele stron na ten temat i niestety nie znalazłem odpowiedzi.
Jeżeli ktoś zna odpowiedz to z góry dziękuje.

tom102 pisze: Jak można obliczyć moduł koła stożkowego o zębach prostych?
Przeszukałem już wiele stron na ten temat i niestety nie znalazłem odpowiedzi.

Części maszyn - Andrzej Rutkowski
lub każdy inny podręcznik traktujący o kołach zębatych

Jak każde inne koło zębate. Dzielisz obwód zewnętrzny na ilość zębów+2, i (w razie niedokładności związanej z pomiarem) bierzesz najbliższy znormalizowany. Ilość zębów z o danym module m(p) koła zębatego jest ściśle powiązana ze średnicą tego koła da,

wynikającą z przekształcenia wzoru:
m = da : z+2
gdzie:
m = moduł zębów koła
da = średnica zewnętrzna koła(wieńca)
z = ilość zębów

W zasadzie dla koła stożkowego (do przekładni o kącie 90°) wzór wyjsciowy na moduł m wygląda tak
Dp = z • mte
gdzie:
Dp - średnica podziałowa zewnętrzna stożka podziałowego
z - rzeczywista ilość zębów w kole
mte - czołowy moduł zewnętrzny
ale ten sam wzór na obliczenie m jak dla koła prostego(powyżej) możemy w praktyce bez wielkiego błędu zastosować do koła stożkowego, z tym że nasze da = Dq(na rysunku poniżej)

czyli: m = Dq : z+2

"Dzielisz obwód zewnętrzny na ilość zębów+2" ? czy średnicę zewnętrzną na (ilość zębów +2)

Witam
dzięki wszystkim za pomoc, zmierzyłem i policzyłem, błąd jest spory ,ale wydaje mi się że, będzie to moduł 3,5.
Problem jest teraz inny, jest ktoś na tym forum kto podejmie się wykonania takiej zębatki jak na zdjęciach.
Mogę ja przesłac jako wzór.
Zębatka współpracuje z większą 50z, przełożenie 1/2

Dziwna ta zębatka, jakaś taka mało płaska
http://pl.wikipedia.org/wiki/Z%C4%99batka

tom102 pisze:zmierzyłem i policzyłem, błąd jest spory

I będzie. Powinienem dopisać że może wyjść spory bo tak naprawdę we wzorze m = Dq : z+2 nie powinno być "2", tylko miedzy ~"1,5" a "2"(co trzeba by dokładnie wyliczyć) bo wysokość głowy zęba(miedzy Dp a Dq) jest funkcją trójkąta prostokątnego (przyprostokątną) ponieważ zarys zęba jest pochylony pod kątem 45° do osi koła

Cezary2528 pisze:Dziwna ta zębatka, jakaś taka mało płaska
http://pl.wikipedia.org/wiki/Z%C4%99batka

Według mnie nie sprawia wrażenia płaskiej, możne zdjęcia trochę ja odchudzają jeszcze bardziej niż brakujące 13 zębów.
Jest to zębatka od posuwu wzdłużnego suportu tokarki na wałku (zresztą od poprzecznego jest taka sama)
Jak będę przy maszynie to porobię zdjęcia całości.

Mam jeszcze jedno pytanie, na zębatce wybity jest numer 35. Co to oznacza?. Na początku myślałem, że chodzi właśnie o moduł 3,5 ale ten sam numer jest tez na innych częściach.

Znacie może kogoś kto by się podjął dorobienia takiej zębatki.

RomanJ4 pisze:

tom102 pisze:zmierzyłem i policzyłem, błąd jest spory

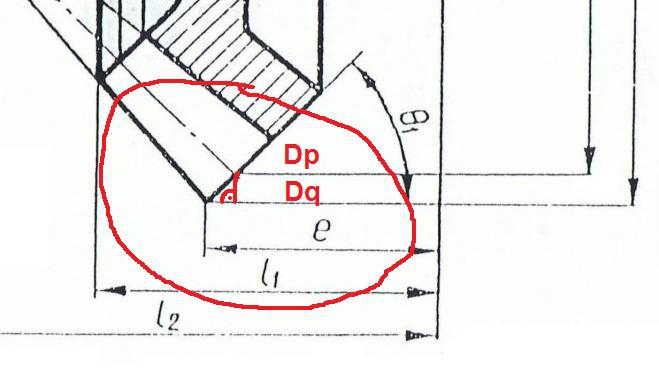
I będzie. Powinienem dopisać że może wyjść spory bo tak naprawdę we wzorze m = Dq : z+2 nie powinno być "2", tylko miedzy ~"1,5" a "2"(co trzeba by dokładnie wyliczyć) bo wysokość głowy zęba(miedzy Dp a Dq) jest funkcją trójkąta prostokątnego (przyprostokątną) ponieważ zarys zęba jest pochylony pod kątem 45° do osi koła

Jeśli przez błąd rozumiecie różnicę między modułem wyliczonym ze wzoru, który podał Roman (m = Dq : z+2 ), a najbliższym znormalizowanym modułem ta zwykle nie wychodzi on jakiś duży i raczej nie pwoinien znacząco odbiegać od najbliższego znormalizowanego.

Przykładowo weźmy jakieś dowolne koło stożkowe , niech będą te z oferty EBMiA i policzmy moduł biorąc średnicę da według ich rysunku . Czyli m=da:z+2
www.ebmia.pl/kola-stozkowe-przelozenie-c-196_56_58.html

Wychodzi zaledwie kilka setek różnicy miedzy modułem policzonym, a tym który można znaleźć w tabeli.

RomanJ4 pisze: ponieważ zarys zęba jest pochylony pod kątem 45° do osi koła

Tak jest, ale tylko gdy przełożenie będzie 1:1 zakładając, że osie kół są do siebie prostopadłe.

Jeżeli będzie inne przełożenie i inna ilość zębów jednego i drugiego koła, to kąt o którym mówimy nie będzie równy 45°, tylko w jednym kole będzie np. 30° a w drugim 60°. I tu chociaż zdjęcia są słabe to nie powiedziałbym żeby miało 45°, tylko raczej mniej.

Kąt ten można sprawdzić z zależności:
σ=arc tg z1/z2
stąd widać że żeby kąt ten miał 45° ,to stosunek z1/z2 (czyli przełożenie) musiałby być równy 1. (tg45°=1)
A tom102 pisze że u niego przełożenie jest . 1/2. A w tym przypadku to mniejsze koło będzie miało 26,5° a drugie większe 63,5°

Ale to tak na marginesie, bo nawet przy innym kącie nie powinno być dużej różnicy między modułem obliczonym i najbliższym znormalizowanym posługując się tym w.w wzorem na moduł jak dla zwykłych kół walcowych.
Może koło mocno zużyte i pomiar średnicy niedokładny lub jakieś nietypowe koło robione w calu.