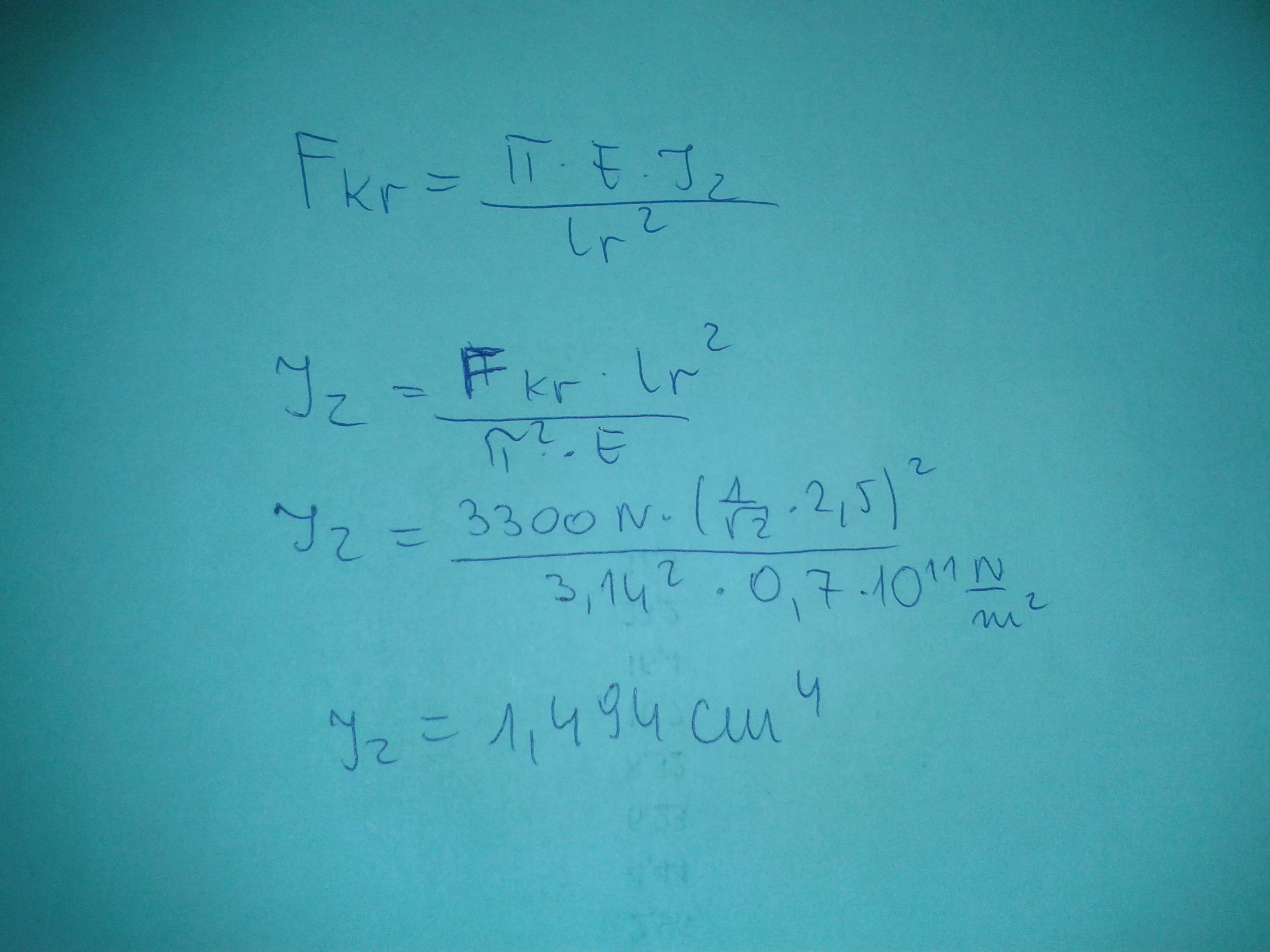ceownik - parametry przekroju , wymiar
-
IWWLI
Autor tematu - Czytelnik forum poziom 1 (min. 10)

- Posty w temacie: 10
- Posty: 17
- Rejestracja: 07 lis 2012, 15:03
- Lokalizacja: POLSKA
ceownik - parametry przekroju , wymiar
Witam , mam wyznaczyć parametry przekroju poprzecznego ceownika i dobrać wymiar znormalizowanych ceowników. Nie wiem jednak od jakich obliczeń zacząć , gdyż nie mam podanych , ani naprężeń , ani żadnych wymiarów. Moimi danymi są siła F , moduł Younga oraz długość L.Bardzo proszę o jakiejś wskazówki...
Ostatnio zmieniony 28 lis 2012, 00:20 przez IWWLI, łącznie zmieniany 1 raz.
Tagi:
-
IWWLI
Autor tematu - Czytelnik forum poziom 1 (min. 10)

- Posty w temacie: 10
- Posty: 17
- Rejestracja: 07 lis 2012, 15:03
- Lokalizacja: POLSKA
owszem.. tylko moim zdaniem brakowało parametrów. Nie wiem , do którego wzoru należało coś podstawić... dalej sobie poradzę , mam tylko problem jak dojść do tego jaki to ceownik.
Z tego wzoru eulerowskiego chciałam wyznaczyć moment bezwł. I , gdzie przyjmuje F=3300N , L=2,5m ,
n=2 ??, jednak wychodzi zbyt małe I , żeby móc wybrać jakiś ceownik..
Z tego wzoru eulerowskiego chciałam wyznaczyć moment bezwł. I , gdzie przyjmuje F=3300N , L=2,5m ,
n=2 ??, jednak wychodzi zbyt małe I , żeby móc wybrać jakiś ceownik..
sorry za pejęzyczenie: liczyszIWWLI pisze:moment bezwładności czy wskaźnik wytrzymalośći?
http://www.matthewz.republika.pl/wyt19.htm
Iz - najmniejszy główny środkowy moment bezwładności przekroju pręta... itd itd
-
pabloid
- ELITA FORUM (min. 1000)

- Posty w temacie: 7
- Posty: 1030
- Rejestracja: 19 paź 2010, 18:53
- Lokalizacja: ~ Kraków
Wzór na wyboczenie jest ten sam, tylko 4 razy trzeba go zastosowac. A to dlatego, że słup jako całość i kazdy z jego elementów ma możliwość wyboczenia się w dwóch kierunkach, co prowadzi nas do:
I. Sprawdzenia wyboczenia elementów gałęzi słupa.
1. po pierwsze nalezy przyjąć, że w każdą galąż słupa idzie połowa siły ociążającej
2. potem dla takiego obciążenia zajmujesz się pojedynczym ceownikiem, który po osi z większym momentem bezwładności ma długość wyboczeniową równą całej wysokości słupa, a po osi z mniejszym momentem bezwładności ma dlugośc wyboczeniową podzieloną na 3 części przewiązkami co doprowadzi cię do obliczenia jednego z dwóch takich samych ceowników biorąc pod uwagę możliwość jego wyboczenia jako części słupa. (dwa warunki bo dwa kierunki wyboczenia- każdemu odpowiada inny moment bezwładności i odpowiednia długość wyboczeniowa)
II. Sprawdzenia wyboczenia słupa jako całości
Traktujesz słup jako całość, wyboczenie liczysz dla całego obciążenia i sumarycznych momentów bezwładności obu ceowników w danym kierunku, a długość wyboczeniową stanowi całość wysokości słupa dla obu kierunków i odpowiadających im momentów bezwładności. (znowu dwa warunki, bo wprawdzie długość wyboczeniowa jest jedna, ale różne są momenty bezwładności)
III ze wszystkich tych 4 warunków wybierasz najniekorzystniejszy tzn wymagający zastosowania największego ceownika. De facto dwa z warunków (dotyczące wyboczenia całości słupa i każdego z ceowników do przodu/tyłu) są tożsame, więc tak naprawdę są 3 warunki do sprawdzenia- bo przy tej samej długości wyboczeniowej pół siły i moment bezwładności jednego ceownika da te same wyniki co cała siła i zsumowane na dany kierunek momenty bezwładności obu ceowników.]
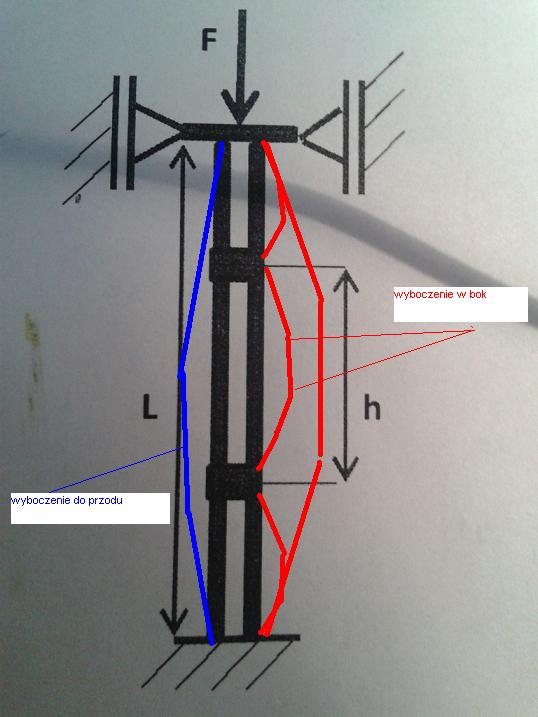
Zauważ też, że masz do czynienia z różnymi warunkami podparcia w różnych przypadkach, (podpory słupa, przewiązki) co z kolei ma wpływ na przyjęcie długości wyboczeniowych. Ciekawie zachowuje się górne podparcie słupa- na boki jak utwierdzenie przesuwne w pionie, a w kierunku przód tył jako albo przegub, albo w ogóle brak podparcia! (musisz się dowiedzieć od autora tego zadania jak potraktować to podparcie w kierunku przód-tył, bo ze schematu ciężko wyrokować) A jakie to ma znaczenie popatrz np tu: http://www.matthewz.republika.pl/wyt19.htm
I. Sprawdzenia wyboczenia elementów gałęzi słupa.
1. po pierwsze nalezy przyjąć, że w każdą galąż słupa idzie połowa siły ociążającej
2. potem dla takiego obciążenia zajmujesz się pojedynczym ceownikiem, który po osi z większym momentem bezwładności ma długość wyboczeniową równą całej wysokości słupa, a po osi z mniejszym momentem bezwładności ma dlugośc wyboczeniową podzieloną na 3 części przewiązkami co doprowadzi cię do obliczenia jednego z dwóch takich samych ceowników biorąc pod uwagę możliwość jego wyboczenia jako części słupa. (dwa warunki bo dwa kierunki wyboczenia- każdemu odpowiada inny moment bezwładności i odpowiednia długość wyboczeniowa)
II. Sprawdzenia wyboczenia słupa jako całości
Traktujesz słup jako całość, wyboczenie liczysz dla całego obciążenia i sumarycznych momentów bezwładności obu ceowników w danym kierunku, a długość wyboczeniową stanowi całość wysokości słupa dla obu kierunków i odpowiadających im momentów bezwładności. (znowu dwa warunki, bo wprawdzie długość wyboczeniowa jest jedna, ale różne są momenty bezwładności)
III ze wszystkich tych 4 warunków wybierasz najniekorzystniejszy tzn wymagający zastosowania największego ceownika. De facto dwa z warunków (dotyczące wyboczenia całości słupa i każdego z ceowników do przodu/tyłu) są tożsame, więc tak naprawdę są 3 warunki do sprawdzenia- bo przy tej samej długości wyboczeniowej pół siły i moment bezwładności jednego ceownika da te same wyniki co cała siła i zsumowane na dany kierunek momenty bezwładności obu ceowników.]

Zauważ też, że masz do czynienia z różnymi warunkami podparcia w różnych przypadkach, (podpory słupa, przewiązki) co z kolei ma wpływ na przyjęcie długości wyboczeniowych. Ciekawie zachowuje się górne podparcie słupa- na boki jak utwierdzenie przesuwne w pionie, a w kierunku przód tył jako albo przegub, albo w ogóle brak podparcia! (musisz się dowiedzieć od autora tego zadania jak potraktować to podparcie w kierunku przód-tył, bo ze schematu ciężko wyrokować) A jakie to ma znaczenie popatrz np tu: http://www.matthewz.republika.pl/wyt19.htm