cnc.info.pl - FORUM CNC

Tak jak w temacie. Muszę skonstruować łuk który jest styczny do okręgu i punktu leżącego poza nim. Jak taki łuk należy narysować?

A co już zrobiłeś i dokładnie z czym masz problem?

Zadaj konkretne pytanie a nie pytaj czy ktoś zrobi za lenia pracę.

Gdybym chciał, żeby ktoś za mnie zrobił prace to prawdopodobnie zwróciłbym się gdzieś indziej, a że zależy mi jednak na zdobyciu pewnej umiejętności to pytam dość ogólnikowo, żebym mógł sobie porawdzić w przyszłości z podobnymi problemami.
Dokładnie chcę poprowadzić łuk przecinający konkrenty punkt P i jest styczny do okręgu. Wygląda to mniej więcej tak:


Nie mogłem znaleźć sposobu konstruowania takiego czegoś, a szukałem w podręczniku T. Dobrzańskiego, gdzie opisanych jest wiele sposobów. Czy ktoś potrafi mi pomóc?
Ten punkt mam dokładnie wytyczony na rysunku, promień szukanego łuku też mam podany.

a w którym punkcie okręgu? Jak w dowolnym to rysujesz od tego punktu na okręgu odcinek do punktu P prostą dzielisz na połowę i przez połowę rysujesz równoległą do tego odcinka Teraz wystarczy wyznaczyć promień i odłożyć go na równoległej do odcinka następnie łuk i już...

łuk o zadanym promieniu R:
W P postaw cyrkiel i narysuj okrąg o promieniu R Twojego łuku.
W środku okręgu postaw cyrkiel i narysuj okrąg o promieniu będącym sumą promieni okręgu i łuku. (R+r)
W środku okręgu postaw cyrkiel i narysuj okrąg o promieniu będącym różnicą promienia łuku i okręgu. (R-r)
Miejsca przecięcia się okręgu P/R z dwoma okręgami wyznaczają zawieszenie łuku stycznego wewnętrznie lub zewnętrznie do okręgu i przechodzącego przez punt P

[ Dodano: 2012-10-26, 00:10 ]
Albo naciśnij klawisz z funkcją points/circle/tan,tan/radius

...

Nzwijmy okrąg do którego stycznej poszukujemy "O"
ustaw cyrkiel na promień poszukiwanego łuku, narysuj okrąg (nazwijmy go nr.1 ) o środku w P, narysuj okrąg nr2 o środku w punkcie przecięcia nr1 i okręgu "O". Jeden z punktów przecięcia okręgów 1 i 2 to poszukiwany środek łuku.
Pytania tego typu przywodzą mi na myśl znany kawał konczący się na "Zmień granice całkowania, zmień granice całkowania" - tylko coś mi się wydaje że pytający jednak nie są profesorami...

A co tam, chciało mi się:

grg12 pisze:Nzwijmy okrąg do którego stycznej poszukujemy "O"
ustaw cyrkiel na promień poszukiwanego łuku, narysuj okrąg (nazwijmy go nr.1 ) o środku w P,..

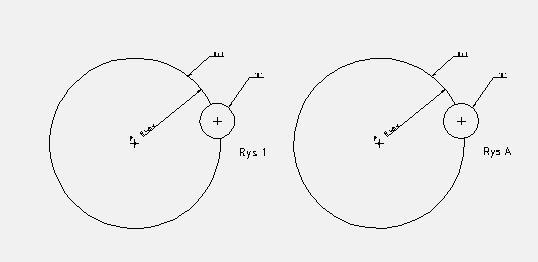
rys 1

qqaz pisze:W P postaw cyrkiel i narysuj okrąg o promieniu R Twojego łuku.

Akurat ustawiło mi się R=107
rys A

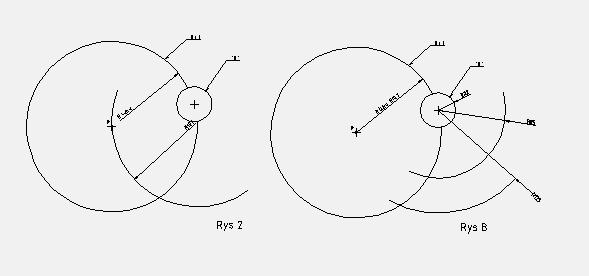
grg12 pisze: narysuj okrąg nr2 o środku w punkcie przecięcia nr1 i okręgu "O" .

Nie wiem jakim promieniem?
Bo jeżeli takim jak łuk to coś nieteges: Rys 2

qqaz pisze:W środku okręgu postaw cyrkiel i narysuj okrąg o promieniu będącym sumą promieni okręgu i łuku. (R+r)
W środku okręgu postaw cyrkiel i narysuj okrąg o promieniu będącym różnicą promienia łuku i okręgu. (R-r)

Fakt, nie zaznaczyłem że tym okregiem jest okręg nr1 - rys B

grg12 pisze: Jeden z punktów przecięcia okręgów 1 i 2 to poszukiwany środek łuku..

kicha rys 3

qqaz pisze:Miejsca przecięcia się okręgu P/R z dwoma okręgami wyznaczają zawieszenie łuku stycznego wewnętrznie lub zewnętrznie do okręgu i przechodzącego przez punt P

rys C





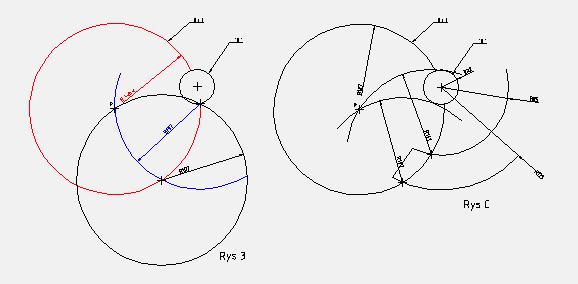
Kol Mitka narysować nie umiem, Poległem tutaj

mitek pisze:prostą dzielisz na połowę i przez połowę rysujesz równoległą

qqaz - masz 100% racji. Pisałem z pamięci zamiast zacząć myśleć